This tutorial will revolve around 3 basic types. A single point, also called a vector; a circle, and an axis-aligned box. I’ll show you the basics of collision detection between them. I’ll also introduce example structs that represent their data.
Basic Types
These are the three types we’ll focus on:
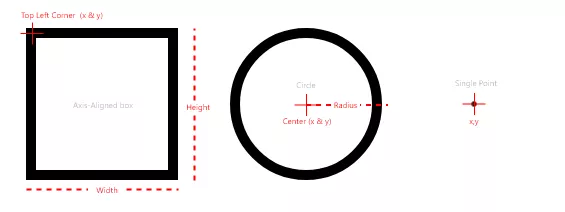
A Single Point
This is the most basic type we’ll cover. A single point. This point can be thought of as a 1×1 square. Code-wise, We just need to track it’s x & y coordinates.
typedef struct Vector2Struct{
int16_t x;
int16_t y;
} Vector2;A Circle
For a circle, we need 2 data pieces:
- The center of the circle
- The radius of the circle.
Instead of using the radius, We’ll use the radius squared. This is because some retro systems (like Game Boy) are not capable of doing a lot of real-time advanced math, and/or do not come with functions like sqrt (square root). The sqrt function is essential in collision detection with circles.
typedef struct CircleStruct{
Vector2 center;
int16_t radiusSquared;
} Circle;
An Axis-Aligned box
An axis-aligned box, sometimes called an “Axis-Aligned Bounding Box”, is Square or Rectangle that has not been rotated. We need three pieces of information:
- Width
- Height
- A corner or the center of the box.
In our example, we’ll use the top left corner. You could use any corner. Alternatively, you could use the center of the box. It’s up to you.
typedef struct AxisAlignedBoxStruct{
Vector2 topLeftCorner;
int16_t width;
int16_t height;
} AxisAlignedBox;Axis-Aligned Box vs. A single point
To check if a box overlaps a single point, we need to make sure the point is on the proper side of each edge. The point should NOT be:
- To the left, of the left edge
- To the right, of the right edge.
- Above the top edge
- Below the bottom edge
If all of these conditions are met, the point is overlapping/inside the box.
NOTE: Some systems have inverted axes. In these systems, increasing a y position makes an object go down.
With a normal system. increasing a y position, makes an object go up:
uint8_t CollisionDetection_AxisAlignedBox_Vector(AxisAlignedBox* box, Vector2* vector){
if(vector->x<box->topLeftcorner.x)return FALSE;
if(vector->x>box->topLeftcorner.x+box->width)return FALSE;
if(vector->y>box->topLeftcorner.y)return FALSE;
if(vector->y<box->topLeftcorner.y-box->height)return FALSE;
return TRUE;
}With an inverted y-axis. increasing a y position, makes an object go down:
uint8_t CollisionDetection_AxisAlignedBox_Vector(AxisAlignedBox* box, Vector2* vector){
if(vector->x<box->topLeftcorner.x)return FALSE;
if(vector->x>box->topLeftcorner.x+box->width)return FALSE;
if(vector->y<box->topLeftcorner.y)return FALSE;
if(vector->y>box->topLeftcorner.y+box->height)return FALSE;
return TRUE;
}The remaining examples will use an inverted y-axis.
Two Axis-Aligned Boxes
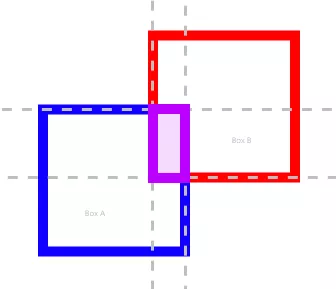
Two check if two axis-aligned boxes are overlapping, we DO NOT have a collision if one of the following conditions are met:
- The left edge of boxA, is to the right of boxB’s right edge.
- The right edge of boxA, is to the left of boxB’s left edge.
- The top edge of boxA, is below boxB’s bottom edge.
- The bottom edge of boxA, is above boxB’s top edge.
uint8_t CollisionDetection_AxisAlignedBox_AxisAlignedBox(AxisAlignedBox* boxA, AxisAlignedBox*
boxB){
if(boxA->topLeftCorner.x>boxB->topLeftCorner.x+boxB.width)return FALSE;
if(boxA->topLeftCorner.y>boxB->topLeftCorner.y+boxB.height)return FALSE;
if(boxA->topLeftCorner.x+boxA.width<boxB->topLeftCorner.x)return FALSE;
if(boxA->topLeftCorner.y+boxA.height<boxB->topLeftCorner.y)return FALSE;
return TRUE;
}Another way to do that, is to use math and the center’s of each box. If the distance between their centers, is less than the sum of their half widths/heights, we have a collision. That might sound confusing, here it is in code form:
uint8_t CollisionDetection_AxisAlignedBox_AxisAlignedBox(AxisAlignedBox* boxA, AxisAlignedBox*
boxB){
int16_t boxAMidX = boxA->topLeftCorner.x+boxA->width/2;
int16_t boxBMidX = boxB->topLeftCorner.x+boxB->width/2;
int16_t minimumDistanceX = boxA->width/2+boxB->width/2;
int16_t xd = boxAMidX-boxBMidX;
if(ABS(xd)>minimumDistanceX)return FALSE;
int16_t boxAMidY = boxA->topLeftCorner.y+boxA->height/2;
int16_t boxBMidY = boxB->topLeftCorner.y+boxB->height/2;
int16_t minimumDistanceY = boxA->height/2+boxB->height/2;
int16_t yd = boxAMidY-boxBMidY;
return ABS(yd)<= minimumDistanceY;
}Two Circles
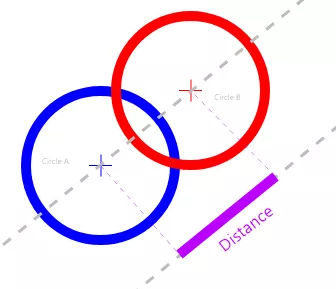
When checking for collision against two circles, we just need to get the squared distance from their centers. If that value, is less than the sum of their two squared radii (plural version of radius), then there is collision.
uint8_t CollisionDetection_Circle_Circle(Circle* circleA, Circle* circleB){
int16_t dx = circleA->center.x-circleB->center.x;
int16_t dy = circleA->center.y-circleB->center.y;
int16_t squaredDistance = dx*dx + dy*dy;
int16_t minimumDistance = circleA->radiusSquared+circleB->radiusSquared;
return squaredDistance<=minimumDistance ;
}Circle vs A single point
Checking for collision with a Circle against a single point, is nearly the same as when checking against two circles. The only difference is we can only use one radius:
uint8_t CollisionDetection_Circle_Vector(Circle* circle, Vector2* vector){
int16_t dx = circle->center.x-vector.x;
int16_t dy = circle->center.y-vector.y;
int16_t squaredDistance = dx*dx + dy*dy;
int16_t minimumDistance = circle->radiusSquared;
return squaredDistance<=minimumDistance ;
}Circle vs Axis-Aligned Box
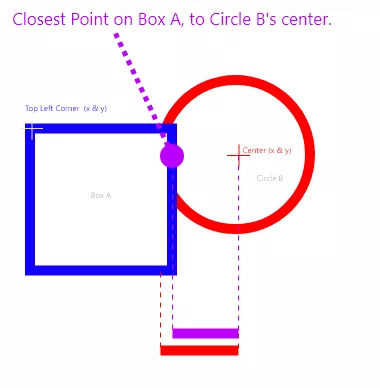
To check if a circle overlaps with an axis-aligned box, we need to find the closest point on the box to the circle’s center. Next we get the distance from that point to the circle’s center. If that distance is greater than the circle’s radius, we have a collision.
Reminder: Because some retro platforms don’t have math equations like sqrt. Instead of using distance and radius, we’re using squaredDistance and radiusSquared.
uint8_t CollisionDetection_Circle_AxisAlignedBox(Circle* circle, AxisAlignedBox* box){
int16_t closestPointOnBoxX = circle->center.x;
int16_t closestPointOnBoxY = circle->center.y;
if(circle->center.x<box->topLeftCorner.x)closestPointOnBoxX=box->topLeftCorner.x;
else if(circle->center.x>box->topLeftCorner.x+box.width)closestPointOnBoxX=box->topLeftCorner.x+box.width;
// This assumes an increasing y position moves an object downwards
// Flip things like before for different systems.
if(circle->center.y<box->topLeftCorner.y)closestPointOnBoxY =box->topLeftCorner.y;
else if(circle->center.y>box->topLeftCorner.y+box.height)closestPointOnBoxY =box->topLeftCorner.y+box.height;
int16_t dx = circle->center.x-closestPointOnBoxX;
int16_t dy = circle->center.y-closestPointOnBoxY;
int16_t squaredDistance = dx*dx + dy*dy;
return squaredDistance<=circle->radiusSquared;
}What about rotated, or more complicated shapes?
I kept this tutorial about the basics. As soon as you introduce more complicated shapes , or rotation; the math and code become significantly more complicated. In such case, you might want to look into a third-party library.